CBSE[DELHI]_X_Mathematics_2019_Set_I
To Access the full content, Please Purchase
-
Q1
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, –3) and B is (1, 4).
Marks:1View AnswerAnswer:
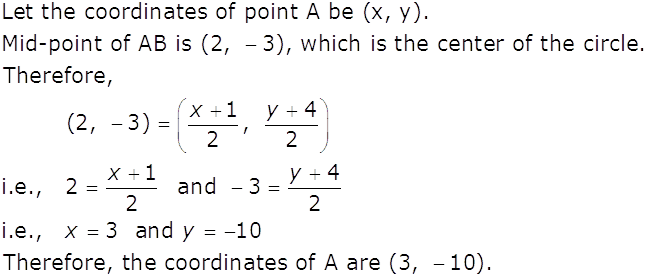
-
Q2
For what values of k, the roots of the equation x2 + 4x + k=0 are real?
Marks:1View AnswerAnswer:

-
Q3
Find the value of k for which the roots of the equation 3x2 – 10x + k = 0 are reciprocal of each other.
Marks:1View AnswerAnswer:
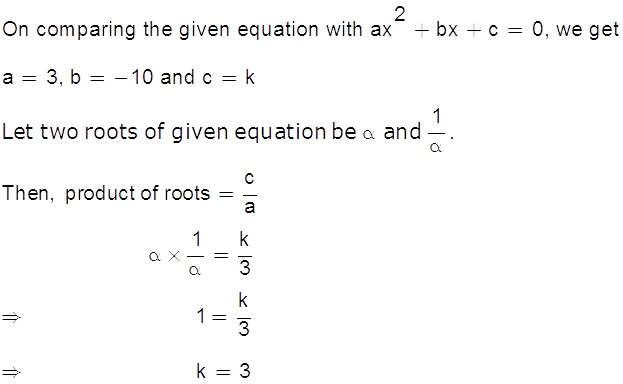
-
Q4
Find A if tan2A = cot(A – 26°).
Marks:1View AnswerAnswer:
tan2A = cot (A – 26°)
cot(90° – 2A) = cot (A – 26°)
90° – 2A = A – 26°
90° + 26° = 3A
A =38.7° (Approx)
-
Q5
Find the value of (sin233° + sin257°).
Marks:1View AnswerAnswer:
sin233° + sin257° = sin233° + sin2 (90 - 33°)
= sin233° + cos2 33°
= 1 [Since, sin2θ + cos2θ = 1]
-
Q6
How many two-digit numbers are divisible by 3?
Marks:1View AnswerAnswer:
The list of two-digit numbers divisible by 3 is:12, 15, 18,. . . 99
Since the difference between two consecutive terms in this list or sequence is same, it is in arithmetic progression (AP).
Here, First term, a = 12, Common difference, d = 3, Last term, an = 99
Since an = a + (n – 1)d
So, 99 = 12 + (n – 1)3
87 = (n – 1)3
n = 29 + 1 = 30
So, there are 30 two-digit numbers that are divisible divisible by 3.
-
Q7
In Fig. 1, DE ǁ BC, AD = 1 and BD = 2 cm. What is the ratio of the ar (Δ ABC) to the ar (Δ ADE)?
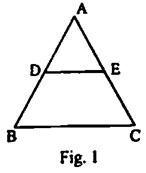
Marks:1View AnswerAnswer:

Therefore, the ratio of the ar (Δ ABC) to the ar (Δ ADE) is 9:1. -
Q8
 Marks:1View Answer
Marks:1View AnswerAnswer:
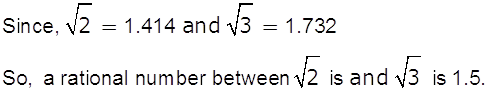
-
Q9
Find the HCF of 1260 and 7344 using Euclid’s algorithm.
Marks:2View AnswerAnswer:
By Euclid’s algorithm:
Considering 1260 as divisor and 7344 as dividend.
7344 = 1260 x 5 + 1044
Considering 1044 as divisor and 1260 as dividend.
1260 = 1044 x 1 + 216
Considering 216 as divisor and 1044 as dividend.
1044 = 216 x 4 + 180
Considering 180 as divisor and 216 as dividend.
216 = 180 x 1 + 36
Considering 36 as divisor and 180 as dividend.
180 = 36 x 5 + 0
Remainder is zero. So, the HCF of 1260 and 7344 is 36.
-
Q10
Show that every positive odd integer is of the form (4q + 1) or (4q + 3), where q is some integer.
Marks:2View AnswerAnswer:
Let ‘a’ be a positive odd integer and b = 4. Now, apply Euclid’s
division algorithm.
a = 4q + rSince 0 ≤ r < 4, the possible remainders are 0, 1, 2 and 3.
That is, a can be 4q, or 4q + 1, or 4q + 2, or
4q + 3, where q is the quotient.However, since ‘a’ is odd, ‘a’ cannot be 4q or 4q + 2
(since, both are divisible by 2).Therefore, any odd integer is of the form 4q + 1 or 4q + 3.



